变直线轨迹等厚振动筛模态分析

    模态分析又被称为固有振动特性分析。模态分析的目的是为了得到结构的固有频率与振型，这是结构分析中的重要参数，因为它们是其他动力学分析的前提，它分析的结果是谐响应分析和瞬态动力学分析以及谱分析的基础。
    由式 (4) 可知，方程最终的形式变为求解矩阵特 征值的问题，质量矩阵 M、刚度矩阵 K 的阶数即固有频率的个数，每一个固有频率对应一组特征向量， 所有的特征向量构成的向量组即是结构的振型。
    用有限元法进行模态分析时，是求解式 (3)，即 求广义特征值问题，ANSYS 有多种分析方法，笔者 采用求解精度高、计算速度快的 Block Lanczos 法进 行求解，计算结果如表 1 所列。
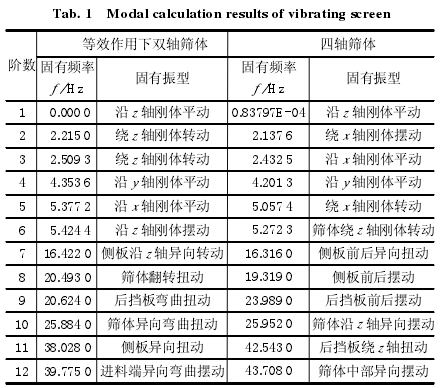    由表 1 对比可知，筛体前 6 阶固有频率对应的振 型是刚体运动，第 6 阶之后是模型的弹性运动，同等 质量同等作用效果下的双轴直线等厚振动筛与四轴变 轨迹等厚振动筛的固有特性有着异同之处：二者的前 6 阶模态振型均为刚性运动，第 7 阶及高阶振型均为弹性振动运动，双轴直线等厚振动筛的固有频率与四 轴变轨迹等厚振动筛的固有频率十分接近，这说明四 轴变轨迹等厚振动筛在一定程度上对双轴直线等厚振 动筛的整体刚度没有影响，反而会有上升的空间，不会降低振动筛自身的破坏的程度。